Table Of Standard Normal Distribution - As an Asian, we are known to be good at mathematics, and one of the essential topics that we have come across in our learning is probability and statistics. As we progress through higher education, we come across the concept of the Standard Normal Distribution Table more often. It is a vital tool used in mathematics, statistics, and probability, and understanding it can make a significant difference in our learning. In this post, we will explore the use of Standard Normal Distribution Table, its importance, and share with you some tips, ideas, and how-to-use it to make your understanding better.
The Normal Distribution Table
What is a Standard Normal Distribution Table?
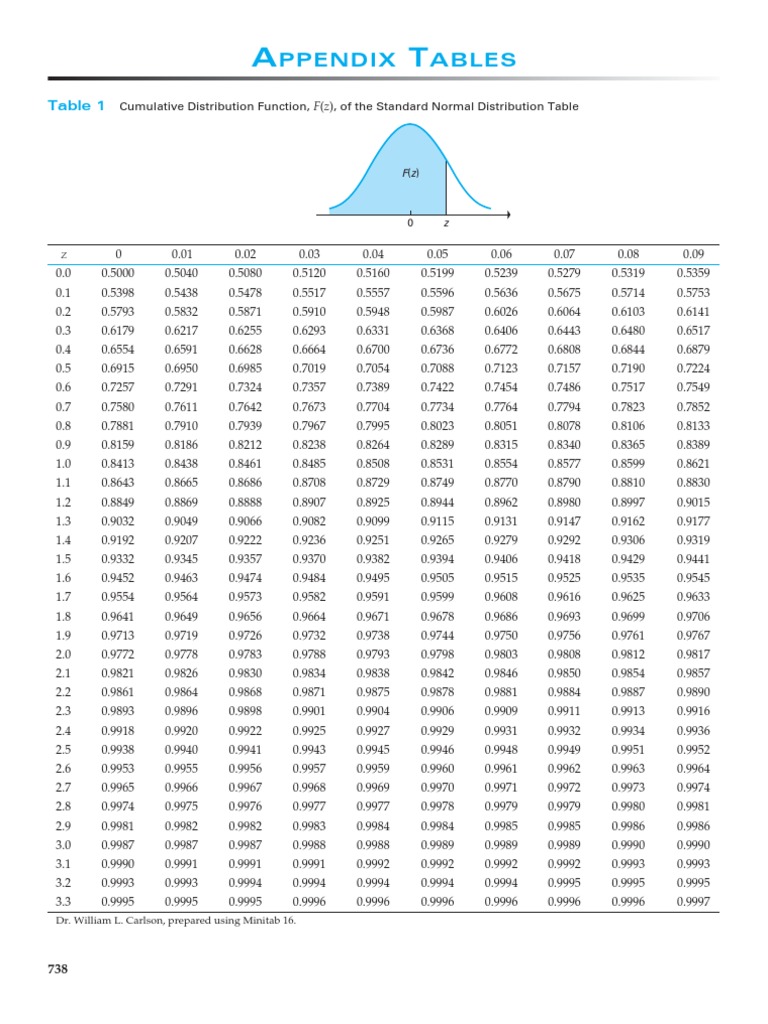
The Standard Normal Distribution Table or Z-table is a table that provides a standardised method of calculating the probability of a particular value within the distribution curve, which has a mean of 0 and a standard deviation of 1. It is an essential tool to find the range, probability, and percentile for any given value.
The Z-table is split into two parts, the positive and the negative parts. Both parts comprise standardised values or Z-scores, which usually range from -3.0 to +3.0. The values in the table denote the area under a bell-shaped curve called the normal distribution curve.
How to use Standard Normal Distribution Table?
Using the Standard Normal Distribution Table can seem a bit daunting at first, and it can be challenging to determine the probability and percentile of a particular value. However, with these tips, you too can master the art of Standard Normal Distribution Table.
Tips and Ideas
- Start by determining the required probability value, percentile, or range.
- Locate the relevant Z-score or standardised value along the top and left-hand side of the table.
- Find the intersection of the relevant Z-score along the top and left-hand side of the table
- Read the value straight down from the intersection point found in step 3
- If the value is negative, convert it to a positive value and locate this value on the negative part of the Z-table
- For values not listed explicitly in the table, it is possible to interpolate to get a good guess of the probability or percentile.
Standard Normal Distribution Table Example
Let us demonstrate how to use the Standard Normal Distribution Table using an example. Suppose we want to find out the probability of obtaining a Z-score of 1.23, which is the standardised Z-score for a particular value x. We can use the Z-table to determine the probability of obtaining a value less than or equal to 1.23.
Begin by identifying the relevant Z-score, which is 1.23
Locate the Z-score on the top of the Z-table and find the first column from the left that is less than or equal to 0.03. For instance, the left-most column is 0.0, and since the value we are using is 1.23, we can continue scrolling to the right until we find 1.2.
We then locate the first two digits of the Z-score in the left-most column of the table. In our case, it is 1.2. Once we have located 1.2 on the table, we find the third digit, which is 0.03, by tracing it down from the top of the table.
The intersection of the row and column headers gives a probability of 0.8907, which specifies that the probability of getting a Z-score equal to or less than 1.23 is 0.8907. This probability is also referred to as the cumulated probability or cumulative distribution function (CDF).
How to Calculate Z-score?
Before we conclude this post, we will also teach you how to calculate Z-score if you are given the mean and standard deviation. Z-score is the measure of how many standard deviations a value is from the mean, and it is calculated using the following formula:
Z = (X - Mean) / Standard deviation
Example:
Suppose we have a dataset with a mean value of 6 and a standard deviation of 3, and we want to find the Z-score of a value 8. We can use the formula, Z = (X - Mean) / Standard deviation, to determine the Z-score
Z = (8 - 6) / 3 = 0.67
The Z-score, in this case, is 0.67, indicating that the value is 0.67 standard deviations above the mean.
Table Of Standard Normal Distribution is an essential tool for every student of mathematics, statistics or probability. Its importance cannot be overemphasized, and its application ranges from finance to medical research. By following the tips, ideas and how-to-use it, you too can master the art of Standard Normal Distribution Table, and it can make a significant difference in your learning.
Read more articles about Table Of Standard Normal Distribution